题目1:
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。1斐波那契(Fibonacci)数列定义如下: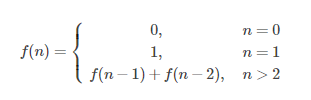
效率很低的解法:
递归解法(效率很低)function Fibonacci_Solution1(n){if(n <= 0)return 0;if(n == 1)return 1;return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);} 2 循环解法:改进的算法:从下往上计算。首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)。。。。。依此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是o(n)。实现代码如下:
function Fibonacci(n){var result[2] = {0 , 1};if(n < 2)return result[n];var fibMinusOne = 1;var fibMinusTwo = 0;var fibN=0;for(var i = 3 ; i <= n ; ++i){fibN = fibMinusOne + fibMinusTwo;fibMinusTwo = fibMinusOne;fibMinusOne = fibN;}return fibN;} 题目2: 一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。1可以把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另一种选择是第一次跳2级,此时跳法数目等于后面剩下n-2级台阶的跳法数目,即为f(n-2)。因此,n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里,不难看出这实际上就是斐波那契数列了。
与斐波那契数列不同的是,其初始值定义稍有不同,
当n=1时,只能跳一级台阶,一种跳法 当n=2时,一次跳一级或两级,两种跳法 所以,关于青蛙跳台阶的定义如下: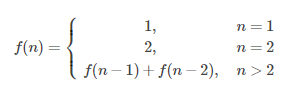
非递归写法
function FrogJump12Step(n){if (n == 1)return 1;if (n == 2)return 2;var frogNMinusOne = 2;//f(n-1)=2var frogNMinusTwo = 1;//f(n-2)=1var frogN = 0;for (unsigned int i = 3; i <= n;++i){frogN = frogNMinusOne + frogNMinusTwo;frogNMinusTwo = frogNMinusOne;frogNMinusOne = frogN;}return frogN;} 递归解法
funciton FrogJump12StepRecursive(n){if (n == 1)return 1;if (n == 2)return 2;return FrogJump12StepRecursive(n - 1) + FrogJump12StepRecursive(n - 2);} 递归式证明:
当n = 1 时, 只有一种跳法,即1阶跳:Fib(1) = 1; 当n = 2 时, 有两种跳的方式,一阶跳和二阶跳:Fib(2) = Fib(1) + Fib(0) = 2; 当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有Fib(3-1)中跳法; 第一次跳出二阶后,后面还有Fib(3-2)中跳法;第一次跳出三阶后,后面还有Fib(3-3)中跳法 Fib(3) = Fib(2) + Fib(1)+Fib(0)=4; 当n = n 时,共有n种跳的方式,第一次跳出一阶后,后面还有Fib(n-1)中跳法; 第一次跳出二阶后,后面还有Fib(n-2)中跳法……………………..第一次跳出n阶后, 后面还有 Fib(n-n)中跳法. Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+……….+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+…….+Fib(n-1) 又因为Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+…….+Fib(n-2) 两式相减得:Fib(n)-Fib(n-1)=Fib(n-1) =====》 Fib(n) = 2*Fib(n-1) n >= 2 递归等式如下: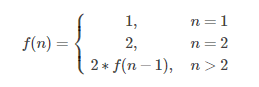
所以:f(n)=2∗f(n−1)=2∗2(n−2)....=2n−1∗f(0)=2n−1f(n)=2∗f(n−1)=2∗2(n−2)....=2n−1∗f(0)=2n−1
非递归解法:function FrogJump12nStep(n){if (n == 1) return 1;else{ var fn1 = 1; var fn = 0; for (var i = 2; i <= n;++i) { fn = 2 * fn1; fn1 = fn; } return fn;}} 递归解法
function FrogJump12nStepRecursive(n){if (n == 1){ return 1;}else if (n == 2){ return 2;}else{ return 2 * FrogJump12nStepRecursive(n - 1);}} 第一步:若第一块矩形竖着放,后边还有n-1个2*1矩形,即此种情况下,有f(n-1)种覆盖方法。
第二部:若第一块横着放,后边还有n-2个2*1矩形,此种情况下,有f(n-2)种覆盖方法。第三部:可得 f(n)=f(n-1)+f(n-2)可知,此题可以转化为其斐波那契数列第n项的值。--------------------- 原文:https://blog.csdn.net/u010177286/article/details/47129019